Intro to Hidden Markov Models: When the State Is Hidden but the Signal Isn't

In Part 1 of this series, we broke down Markov Chains and Markov Decision Processes, two models for fully observable systems. But what happens when the thing you’re trying to model can’t be directly observed?

That’s where Hidden Markov Models (HMMs) come in. These models are essential for making sense of systems where the outcome is visible, but the cause is hidden, like identifying parts of speech in a sentence, or guessing the weather based on how many ice creams someone eats.

What Makes a Markov Model "Hidden"?

Hidden Markov Models are built for partially observable, autonomous systems. That means:

• You can’t directly see the underlying state (e.g. is the day hot or cold?)
• But you can observe signals that depend on those hidden states (e.g. how many ice creams someone eats)

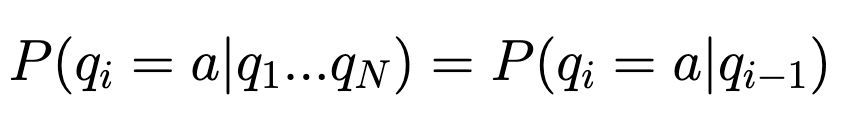
Like other Markov models, HMMs assume that:

1. The next state depends only on the previous state (the Markov assumption)
2. The current output depends only on the current state, not on previous outputs (the output independence assumption)

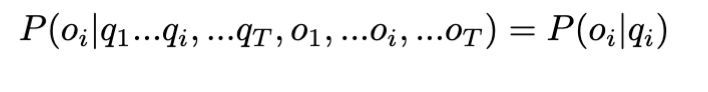
Key Components of an HMM

Much like Markov Chains, an HMM has a set of states, a transition probability matrix, and an initial probability distribution. Unlike Markov Chains, however, an HMM includes what we call emission probabilities, or the probability that an observation oi is generated at state qi. An HMM builds on the same structure as a Markov Chain but adds one key ingredient:

• States (Q) – Hidden variables, like “Hot” or “Cold”
• Observations (O) – Visible outputs, like “3 ice creams”
• Transition Probabilities (A) – The chance of moving between hidden states
• Emission Probabilities (B) – The chance of observing something, given a hidden state
• Initial State Probabilities (π) – The starting probabilities for hidden states

The Three Core Problems of HMMs

According to foundational work by Rabiner (1989) and Ferguson (1960s), working with HMMs usually involves solving one of three key problems:

1. Likelihood – What’s the probability of observing a given sequence? Use the Forward algorithm.
2. Decoding – What’s the most likely sequence of hidden states behind a series of observations? Use the Viterbi algorithm.
3. Learning – Given the observations and known states, what are the best model parameters? Use the Forward-Backward or Baum-Welch algorithm.

A Classic Example: Jason and the Ice Creams

Let’s look at a fun example from Jason Eisner (2002). Suppose we want to figure out whether a day was hot or cold, not by checking the weather report, but by tracking how many ice creams Jason ate.

Here’s our observation sequence:

3 ice creams, 1 ice cream, 3 ice creams

We don’t know the actual weather. That’s hidden. But we can build a trellis diagram to estimate the most likely state sequence based on emissions (ice cream counts) and our known model parameters.

The trellis has:

• Rows = Hidden states (e.g. Hot, Cold)
• Columns = Observed days
• Edges = Probabilities of state transitions and emissions

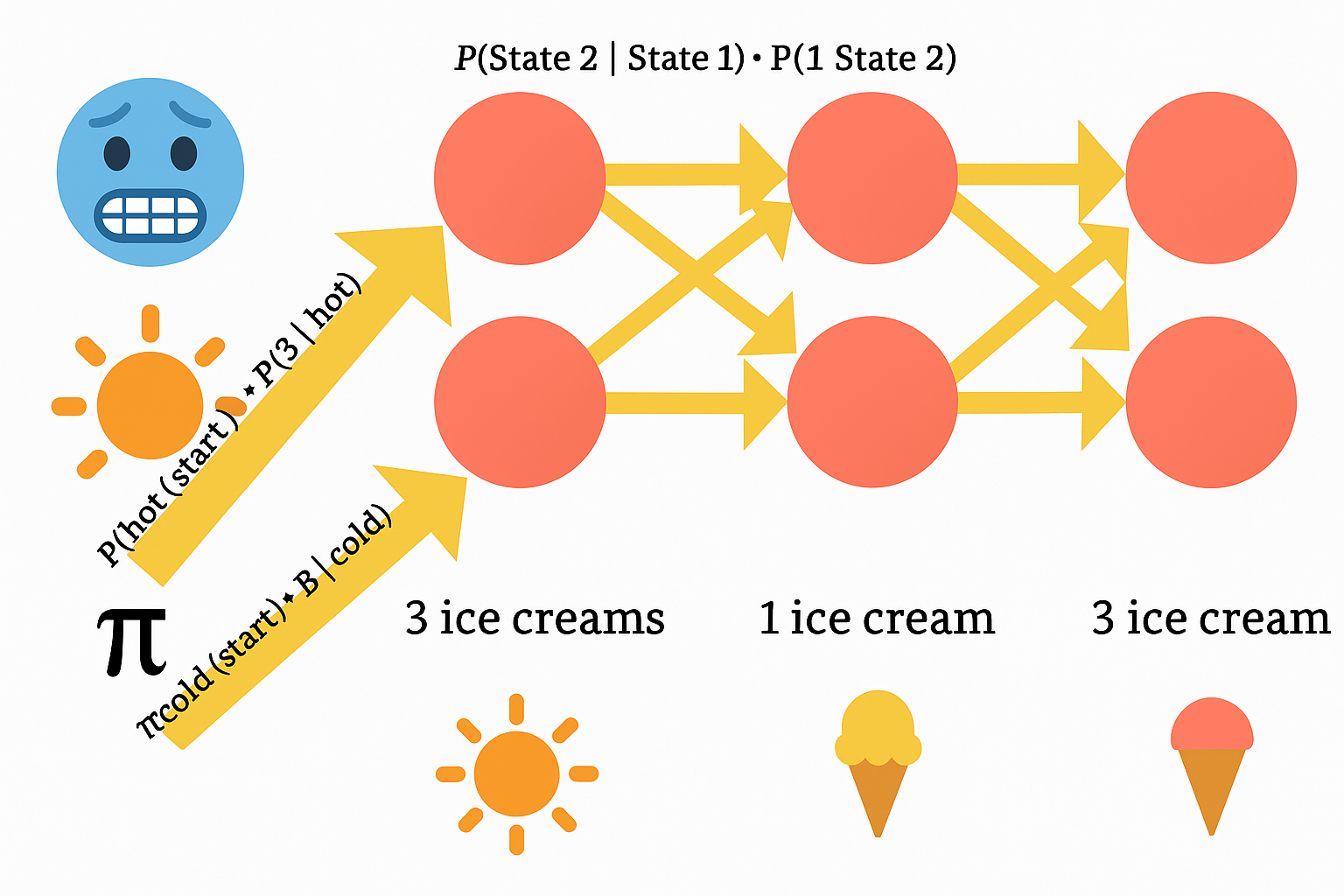
Depending on the algorithm we apply:

• The Forward algorithm adds up probabilities across all paths to compute how likely the sequence is overall.
• The Viterbi algorithm finds the single best path through the trellis by taking the highest probability at each step and tracing it backward.
• The Forward-Backward algorithm learns the best model parameters by iteratively refining estimates.

Why Hidden Markov Models Matter

HMMs were a foundational tool in early NLP and speech recognition systems and they still underpin concepts in modern sequence modeling. They allow us to:

• Infer hidden patterns from noisy or indirect signals
• Build generative models of sequence data
• Understand how probability flows through time, even when some of that flow is hidden

Whether you're modeling human behavior, decoding audio signals, or aligning tokens in language tasks, the HMM framework offers a powerful starting point. If you’re working on sequence-based problems, from chatbot interactions to biological data, these models can help you build intuition, and structure, for reasoning under uncertainty.

Watch the full explainer video below: